इस लेख में हम समद्विबाहु त्रिभुज का क्षेत्रफल का सूत्र व समद्विबाहु त्रिभुज का परिमाप का सूत्र (फॉर्मूला), परिभाषा क्या है।(samdibahu tribhuj ka kshetrafal ka sutra formula) के बारे में यहां पर बताया गया।
समद्विबाहु त्रिभुज किसे कहते हैं?क्या है।
सामान्यत त्रिभुज के तीन प्रकार होते है उन्हीं में से एक है समद्विबाहु त्रिभुज । तो चलिए जानते है समद्विबाहु त्रिभुज किसे कहते है।
समद्विबाहु त्रिभुज की परिभाषा :-
वह त्रिभुज जिसकी तीन भुजाओं में से कोई दो भुजाएं समान होती है। समद्विबाहु त्रिभुज कहलाता है।
- समद्विबाहु त्रिभुज की असमान भुजा आधार होती है।
- त्रिभुज की दोनों समान भुजाओं के कोण भी समान होते है।
समद्विबाहु त्रिभुज का क्षेत्रफल (samdibahu tribhuj ka kshetrafal)
समद्विबाहु त्रिभुज का क्षेत्रफल से तात्पर्य है कि किसी Samdibahu Tribhuj के समान आकृति या वस्तु द्वारा घेरा गया क्षेत्र , समद्विबाहु त्रिभुज का Kshetrafal कहलाता है।
समद्विबाहु त्रिभुज का क्षेत्रफल का सूत्र (Formula)
समद्विबाहु त्रिभुज का क्षेत्रफल (samdibahu tribhuj ka kshetrafal) ज्ञात करने का फॉर्मूला निम्नलिखित है।
जैसा कि हम पता है कि एक समद्विबाहु त्रिभुज की दो भुजाएं समान और एक भुजा असमान होती है। तो माना त्रिभुज की असमान भुजा की लंबाई a है और दोनों समान भुजाओं की लंबाई b है तो
समद्विबाहु त्रिभुज का क्षेत्रफल का सूत्र :-
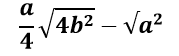
जहां :-
a :- असमान भुजा की लंबाई
B :- समान भुजाओं की लंबाई
Example :- किसी समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात करो जिसकी तीनों भुजाओं का माप क्रमश: 12 cm, 18 cm , 12 cm है।
हल :-
यहां पर दिया गया है कि दो समान भुजाओं का माप = 12cm है
असमान भुजा का माप 18 cm हैं।
अत Samdibahu Tribhuj Ka Kshetrfal के सूत्र से
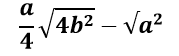
b2 = 12× 12 = 144
a2 = 18 × 18 = 324
का मान सूत्र में रखने पर
18/4 [ (√4×144) – (√ 324) ]
= 18/4 [√576 -√324]
= 9/2 [24-18]
= 9/2 × 6 = 27 cm2
अत त्रिभुज का क्षेत्रफल 27 cm2 है।
इस सूत्र के सहायता से हम त्रिभुज का क्षेत्रफल ज्ञात कर सकते है। इस सूत्र से संबंधित विभिन्न उदाहरण नीचे दिए गए है।
समद्विबाहु त्रिभुज का परिमाप
समद्विबाहु त्रिभुज का परिमाप से तात्पर्य है कि त्रिभुज की तीनों भुजाओं की लंबाई का योग।
अर्थात एक samdibahu tribhuj ka parimap उसकी दो समान व असमान भुजा की लंबाई का योग होता है।
समद्विबाहु त्रिभुज के परिमाप का सूत्र :-
जैसा कि हमें ज्ञात है कि त्रिभुज की असमान भुजा का की लंबाई a और दोनों समान भुजाओं की लंबाई b है तो samdibahu tribhuj ka parimap का सूत्र निम्न होगा
समद्विबाहु त्रिभुज के परिमाप का सूत्र :-
असमान भुजा की लंबाई + समान भुजाओं की लंबाई
= a + (b+b) = a + 2b
Example :- यदि एक समद्विबाहु त्रिभुज की तीनों भुजाओं का माप क्रमश 10 cm, 15 cm व 15 cm है तो परिमाप ज्ञात करे।
हल :-
समद्विबाहु त्रिभुज के परिमाप के सूत्र से :-
= a +2b
= 10+15+15
= 40 cm (उतर)
समद्विबाहु त्रिभुज के गुणधर्म :-
- इसकी दो भुजाएं समान होती है।
- समान भुआजो के कोण भी समान होते है।
- असमान भुजा इसमें सामान्यता आधार होती है।
अन्य अध्ययन सामग्री
वास्तविक संख्या किसे कहते हैं? परिभाषा (What is Real Number In Hindi) कक्षा 10
त्रिभुज का क्षेत्रफल का सूत्र उदाहरण Tribhuj ka Kshetrafal ka Formula (Chetrafal)
समबाहु त्रिभुज का क्षेत्रफल एवं परिमाप का सूत्र | समबाहु त्रिभुज का परिमाप
त्रिभुज की परिभाषा एवं त्रिभुज के प्रकार, गुण – Triangle In Hindi(types Formula)
समद्विबाहु त्रिभुज के क्षेत्रफल से संबंधित प्रश्न (उदाहरण)
उदाहरण (1) :- दो समद्विबाहु त्रिभुज के संगत कोण बराबर है तथा इनके क्षेत्रफल का अनुपात 25:36 है तो इनकी संगत ऊंचाइयों का अनुपात क्या होगा।
- (a) 25:36
- (b) 36:25
- (c) 5:6
- (d) 6:5
उतर :- (d)
उदाहरण (2) :- किसी त्रिभुज में भुजाओं का योग सदैव होगा :-
- (a) तीसरी भुजा से छोटा
- (b) तीसरी भुजा से बड़ा
- (c) तीसरी भुजा के बराबर
- (d) तीसरी भुजा का दो तिहाई
उतर :- (b)
उदाहरण (3) :- किसी त्रिभुज के दो कोणों का अनुपात 4:5 है यदि इन कोणों का योग के बराबर हो तो तीसरे कोण का मान कितना होगा।
- (a) 80
- (b) 40
- (c) 50
- (d) 90
उतर :- (d)
उदाहरण (4) :- एक व्यक्ति पहले 150 मीटर पूर्व की ओर जाता है और उसके बाद 200 मीटर उतर की ओर जाता है। वह अपनी मूल स्थिति की से कितनी दूर है?
- (a) 350 मीटर
- (b) 250 मीटर
- (c) 50 मीटर
- (d) 625 मीटर
उतर :- (b)
उदाहरण (5) :- किसी त्रिभुज के तीनों शिर्षों से विपरीत भुजाओं पर डाला गए लंब के प्रतिछेद बिंदु उस त्रिभुज का कोनसा केंद्र है।
- (a)केद्रक
- (b)लंब केंद्रक
- (c)अंत केंद्र
- (d)परिकेंद्र
उतर :- (b)
उदहारण (6):- उस त्रिभुज का क्षेत्रफल ज्ञात करो जिसकी भुजा क्रमश 12, 20, 12 cm हो।
उदाहरण :-(7) उस Samdibahu tribhuj का क्षेत्रफल का ज्ञात करे जिसकी भुजाएं क्रमश 15cm,22cm,15cm है।
समद्विबाहु त्रिभुज का परिमाप से संबंधित प्रश्न
उदाहरण (1) :- उस त्रिभुज का परिमाप ज्ञात करो जिसकी भुजाओं का माप 5,6,5 cm है।
उतर 5+6+5= 16cm
केंद्रक :- किसी त्रिभुज की मधिकाओ का प्रतीछेद बिंदु त्रिभुज का केंद्रक कहलाता है।
लंब केंद्र :- किसी त्रिभुज के प्रत्येक शीर्ष से विपरीत भुजा पर डाले गए लंबो का प्रतिछेड़ बिंदु उसका लंब केंद्र कहलाता है।